问题
找一个 zero-range effective model 来重复出低能散射的性质, 比如 低能散射态的相移和 shallow bounded state .
Pseudopotential
Intro
这个 pseudopotential 应该形式简单. 最先考虑的是 Dirac delta function .
它应该能够得到如下波函数
$$\begin{align} \psi(r\to 0) \sim \frac{\sin(kr + \delta_{k} )}{r} \end{align}$$Dirac Delta Function
Equation
取 pseudopotential 为
$$\begin{align} V_{\mathrm{ps}}(\vec{r}) = g \delta^3(\vec{r}) \end{align}$$代入 Schrodinger eq
$$\begin{align} \left[ -\frac{\hbar^2}{2\mu}\nabla^2 +V_{\mathrm{ps}(\vec{r})} \right] \psi(\vec{r}) = E \psi(\vec{r}) \end{align}$$Dirac Delta Function 的性质体现在积分中, 所以对上式在无穷接近零点的无 穷小体积内积分
$$\begin{align} -\frac{\hbar^2}{2\mu}\int_{r < \varepsilon}\nabla^2\psi \cdot \mathrm{d}\vec{r}^3 + g \psi(r=0) = E \int_{r < \varepsilon}\psi(\vec{r})\cdot\mathrm{d}^3\vec{r} \end{align}$$左边第一项
方程左边第一项可以用 Gauss 定理 ( 散度定理, 即, 对一个矢量场的面积分等 于对其散度的体积分), 得到
$$\begin{align} \int \nabla \cdot (\nabla\psi) \mathrm{d} \vec{r}^3 = \int \nabla \psi \cdot \mathrm{d}\vec{S} \end{align}$$下面计算 $\nabla\psi$ . 要求的是在 $r\to 0$ 时的结果, 所以可以对 $\psi$ 在 $r\to 0$ 展开, 分析 leading order
$$\begin{align*} \psi \sim& \frac{\sin kr \cos \delta_k + \cos kr \sin \delta_k}{r} \\ = & k\cos\delta_k - \frac{k^3\cos\delta_k}{3!}r^2 +\sin\delta_k\frac{1}{r} - \frac{k^2\sin\delta_k}{2}r + \mathcal{O}(r^3) \end{align*}$$对第一项常数项的散度是 $0$ .所以
$$\begin{align} \nabla\psi \sim -\frac{k^3\cos\delta_k}{3!}\cdot 2 \vec{r} -\sin\delta_k\cdot \frac{\vec{r}}{r^3} - \frac{k^2\sin\delta_k}{2}\cdot \frac{\vec{r}}{r} \end{align}$$对面积积分
$$\begin{align*} \int_{r < \varepsilon} \nabla \psi \cdot \mathrm{d}\vec{S} =& -\frac{k^3\cos\delta_k}{3!}\cdot 2\cdot \varepsilon \cdot 4\pi \varepsilon^{2} \\ &- \sin \delta_k \cdot \frac{4\pi\varepsilon^2}{\varepsilon^{2}} \\ &- \frac{k^2\sin\delta_k}{2}\cdot 4\pi\varepsilon^2 \end{align*}$$可以看出, 当 $\varepsilon\to 0$ 时, 第一项和第三项都以 $\varepsilon^{2}$ 的速度 $\to 0$ , 只有第二项存在, 所以
$$\begin{align} \int \nabla \cdot (\nabla\psi) \mathrm{d} \vec{r}^3 \sim -4\pi\sin\delta_k \end{align}$$左边第二项
方程左边第项是常数项
右边第一项
当 $r\to 0$ 时, 波函数是一个有限的值. 对一个有限的值在无穷小体积内积分, 结果是 $0$
结论
所以积分完得到
$$\begin{align} \frac{\hbar^2}{2\mu}\cdot 4 \pi \cdot \sin \delta_k + g \frac{\sin(kr + \delta_k)}{r}|_{r=0} = 0 \end{align}$$可以看出, 只要 $\delta_k$ 是有限的值, 第二项就是发散的. 所以, 如果用 Dirac Delta Function 做 pseudopotential 的话, 只允许散射相移是 $0$ .
解释
Pseudopotential 模拟有限深方势阱的散射长度
最初的问题是用一个 pseudopotential 来模拟重复出低能散射的的性质, 比如 散射长度. 如果我们用一个 Dirac 势来模拟一个有限深方势阱的散射长度, 也 就是让一个 Driac 势得到和有限深方势阱的散射长度 $a_s$ . 这样, 应该让 $r_0$ 变小, 同时 $V_0$ 变大, 来使它变得像一个 Dirac 势, 同时使得散射长度 $a_s$ 保持不变. 在两体散射中, 已经求得了低 能条件下的散射长度 $a_s$ 和势阱深度 $V_0$ 之间的定量关系
$$\begin{align} \frac{a_s}{r_0} = 1 - \frac{\tan(\sqrt{\tilde{V}_0})}{\sqrt{\tilde{V}_0}} \end{align}$$其中 $\tilde{V}_0 = \frac{V_0}{\hbar^2/(2\mu r_0^2)}$ 对于 Dirac 势来说, $r\to 0$ , 若要保持 $a_s$ 固定不变,那么等式左边的 $\frac{a_s}{r_0}$ 就要变成一个发散的值. 这恰好对应散射共振所对应的势阱 深度. 散射共振时势阱深满足
$$\begin{align} \tilde{V}_0 = \frac{V_0}{\hbar^2/(2\mu r_0^2)} = \left(\frac{\pi}{2}\right)^2 \end{align}$$上式可以看出, 对于 $r\to 0$ 的 Dirac 势来说, $V_0$ 应该以 $r_0^2$ 的速度 $\to\infty$ , 才能保持 $a_s$ 是一个有限的值.
矛盾之处
以上所做的, 就是用一个 $g\delta^3(\vec{r})$ 代替了
$$\begin{align*} V(r) = \left\{ \begin{aligned} 0 & , r > r_0 \\ -V_0 & , r < r_0 \end{aligned} \right. \end{align*}$$如果二者是等价的的, 那么对它们在全空间的积分应该是相等的, 即
$$\begin{align} g\int\delta^3(\vec{r}) \cdot \mathrm{d}^3\vec{r} = \int V(r) \cdot \mathrm{d}^3\vec{r} \end{align}$$结果为
$$\begin{align} g = V_0\cdot \frac{4\pi r_0^3}{3} \end{align}$$$g$ 是一个有限的常数, 那么 $V_0$ 应当以 $r_0^{3}$ 的速度 $\to \infty$ .
而前面的结论是 $V_0$ 应该以 $r_0^2$ 的速度 $\to\infty$ , 才能保持 $a_s$ 是一 个有限的值. 也就是说, Dirac 势的 $V_0 \to \infty$ 的速度过快.
有限深方势阱的结论和前面 general 的讨论结论是一致的: pseudopotential $g\delta^3(\vec{r})$ 不能重复出低能散射的性质.
李黄杨 Pseudopotential
思路
式
$$\begin{align} \frac{\hbar^2}{2\mu}\cdot 4 \pi \cdot \sin \delta_k + g \frac{\sin(kr + \delta_k)}{r}|_{r=0} = 0 \end{align}$$中, 发散出现在左边第二项中, 如果把 $g$ 换成一个常数加一个算符, 发散就可以消除.
李黄杨 Pseudopotential
李黄杨 Pseudopotential 将 $g\delta^3 (\vec{r}) \to g \delta^3 (\vec{r})\frac{\partial}{\partial r}r$ ,式子变为
$$\begin{align} \frac{\hbar^2}{2\mu}\cdot 4 \pi \cdot \sin \delta_k + g k\cos \delta_k = 0 \end{align}$$那么
$$\begin{align} g = -\frac{\tan \delta_k}{k}\cdot\frac{2\pi\hbar^2}{\mu} = \frac{2\pi\hbar^2a_s}{\mu} \end{align}$$Renomalizable Contact Potential
问题
李黄杨 Pseudopotential 在解少体问题时是方便的, 但是也有很多情况下, 用 李黄杨 Pseudopotential 是不方便的. 比如, 研究 Many-Body Physics , 一般 在热力学极限, 即, 粒子数 $N\to \infty$ , 体积 $V \to \infty$ , 密度 $n \to \mathrm{const.}$ 的情况下, 在实空间用一次量子化的形式是很难处理地. 在 多体中通常是写一个二次量子化的 Hamiltonian . 但是 李黄杨 Pseudopotential 中奇怪的算符处理起来会很麻烦. 所以还是会用一个简单地 $g\delta^3(\vec{r})$ . 发散会通过重整化来进行处理.
Hamiltonian
$$\begin{align*} \hat{H} =& \int d^3\vec{r} \cdot\left[ \psi^{\dagger}(\vec{r}) \left( -\frac{\hbar^2}{2m}\nabla^2 \right)\psi(\vec{r}) \right] + \frac{1}{2}\int \mathrm{d}^3\vec{r} \int \mathrm{d}^3\vec{r}'\cdot \psi^{\dagger}(\vec{r})\psi^{\dagger}(\vec{r}') \cdot g \delta^3(\vec{r} - \vec{r}') \cdot \psi(\vec{r}')\psi(\vec{r}) \\ =& \int d^3\vec{r} \cdot\left[ \psi^{\dagger}(\vec{r}) \left( -\frac{\hbar^2}{2m}\nabla^2 \right)\psi(\vec{r}) \right] + \frac{1}{2}g\int \mathrm{d}^3\vec{r} \cdot \psi^{\dagger}(\vec{r})\psi^{\dagger}(\vec{r}) \cdot \psi(\vec{r})\psi(\vec{r}) \end{align*}$$T-matrix
处理方法一: 将散射问题作为含时微扰, 求质心系相对运动的 T-matrix
T-matrix 的表达式( Supplementary 中有推导 )为
$$\begin{align} T = V + V \frac{1}{E_i-H_0 +\mathrm{i}0^{ +}} T \end{align}$$$E_i$ 是入射能量. 它对应的物理图像是单粒子把势 $V$ 作为含时微扰. 如果写 出 T-matrix 在 $\vec{k}$ 空间中的表达式的话, 只有 on-shell 的 T 是有意 义的.
本问题是一个两体问题, 但是可以在质心系中只考虑相对运动, 所以上式适用于 本问题. 下面计算它在 $\vec{k}$ 空间中的表达式
$$\begin{align} \langle \vec{k} |T |\vec{k}'\rangle = \langle \vec{k} |V |\vec{k}'\rangle + \langle \vec{k} |V \frac{1}{E_{\vec{k}'}-H_0 + \mathrm{i}0^+} T|\vec{k}'\rangle \end{align}$$上式中的 $T, V$ 都是算符. 下面分别计算各项.
第一项
已经知道了算符 $V$ 在坐标表象是对角的, 也就是
$$\begin{align} V | \vec{r} \rangle = g \delta^3(\vec{r}) | \vec{r}\rangle \end{align}$$那么就可以插一组坐标表象的完备基
$$\begin{align*} \langle \vec{k} |V |\vec{k}'\rangle =& \int \mathrm{d}^3\vec{r} \cdot\langle \vec{k} | V | \vec{r}\rangle \langle \vec{r}|\vec{k}'\rangle \\ = & g \int \mathrm{d}^3\vec{r}\cdot\delta^3(\vec{r}) \cdot \frac{1}{v} e^{\mathrm{i}(\vec{k}'-\vec{k})\cdot \vec{r}} \\ = & \frac{g}{v} \end{align*}$$这里 $\vec{k}$ 空间的本征态取箱归一化, 即 $\langle \vec{r} | \vec{k} \rangle = \frac{1}{\sqrt{v}}e^{\mathrm{i}\vec{k}\cdot \vec{r}}$ , $v$ 代表体积.
第二项
算符 $V$ 在 $\vec{k}$ 空间的形式前面已经求出, 且 $|\vec{k}\rangle$ 也是 $H_0$ 的本征态, 所以考虑插入一组 $\vec{k}$ 空间的完备基
$$\begin{align*} &\langle \vec{k} |V \frac{1}{E_{\vec{k}'}-H_0 + \mathrm{i}0^+} T|\vec{k}'\rangle\\ = & \sum_{\vec{k}''}\langle \vec{k} |V| \vec{k}'' \rangle \langle \vec{k}'' | \frac{1}{E_{\vec{k}'}-H_0 + \mathrm{i}0^+} T|\vec{k}'\rangle \\ = & \sum_{\vec{k}''} \frac{g}{v} \frac{1}{E_{\vec{k}'}-\frac{\hbar^2k''^2}{2\mu} + \mathrm{i}0^+}\langle \vec{k}'' | T|\vec{k}'\rangle \end{align*}$$结果
将上面的计算结果代入原式
$$\begin{align} \langle \vec{k} |T |\vec{k}'\rangle = \frac{g}{v} + \frac{g}{v}\sum_{\vec{k}''} \frac{1}{E_{\vec{k}'}-\frac{\hbar^2k''^2}{2\mu} + \mathrm{i}0^+}\langle \vec{k}'' | T|\vec{k}'\rangle \end{align}$$从上式可以看出, $\langle \vec{k} |T |\vec{k}'\rangle$ 的取值与 $\vec{k}$ 的取值无 关, 因为等式右边没有出现 $\vec{k}$ . 将 $E_{\vec{k}'}$ 简记为 $E$ , 则 $\langle \vec{k} |T |\vec{k}'\rangle$ 的取值只与 $E$ 有关. 所以上式可以写为
$$\begin{align} T(E) = \frac{g}{v} + \frac{g}{v}\sum_{\vec{k}} \frac{1}{E-\frac{\hbar^2k^2}{m} + \mathrm{i}0^+} T(E) \end{align}$$其中将约化质量化回了粒子的质量 $\mu = m/2$ .
移项就得到了最终的表达式
$$\begin{align*} T(E) = \frac{1}{\frac{v}{g}- \sum_{\vec{k}}\frac{1}{E - \frac{\hbar^2k^2}{m}+\mathrm{i}0^+}} \end{align*}$$处理方法二: 通过 Feynman 图方法求解 T-matrix
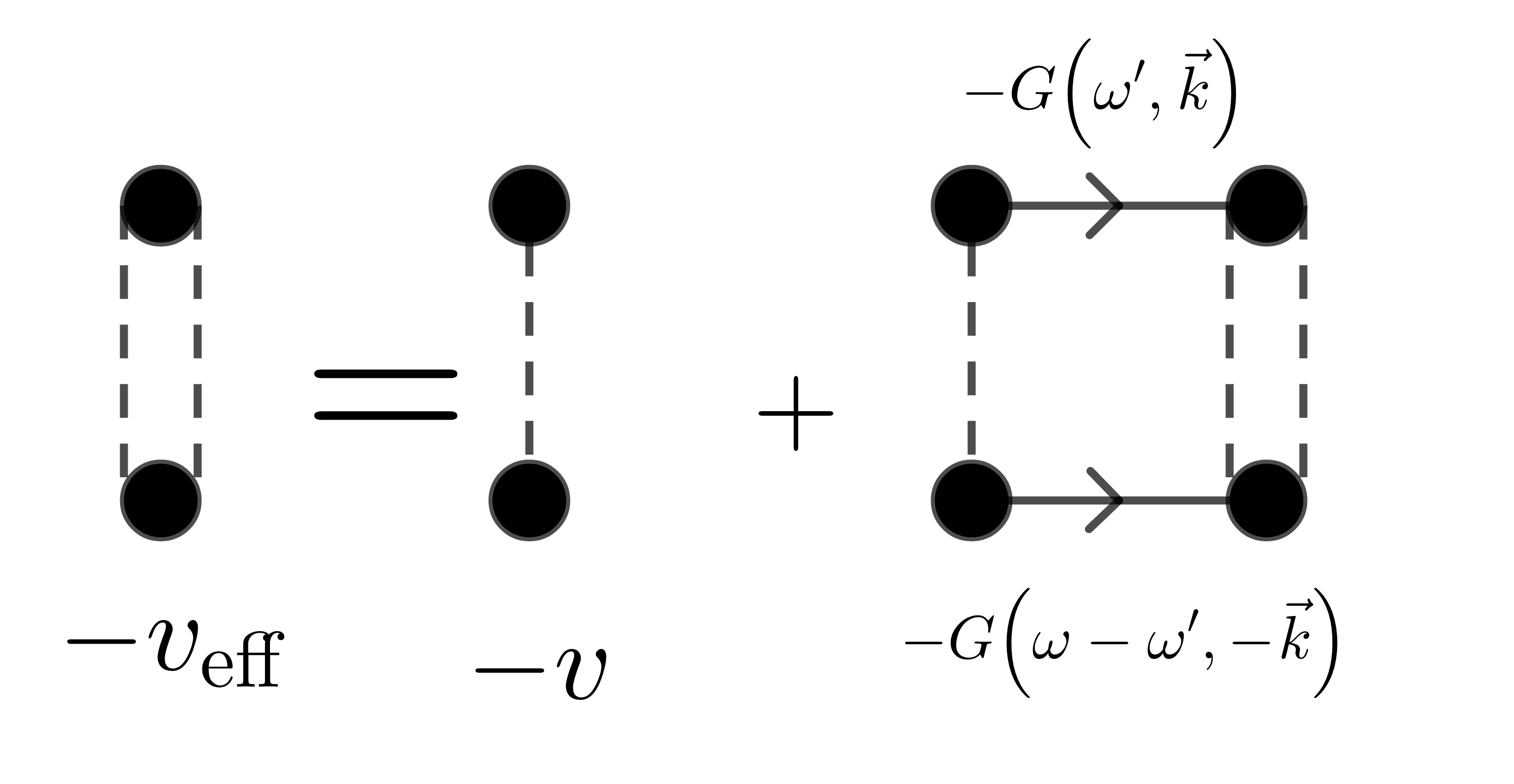
T-matrix 可以看作是有效相互作用, 上图对应为
$$\begin{align} -v_{\mathrm{eff}} = -v + (-v) \frac{1}{\beta}\sum_{\vec{k}} \sum_{\omega'} \left(-G(\omega', \vec{k})\right) \left(-G(\omega-\omega', -\vec{k})\right) \left(-v_{\mathrm{eff}}\right) \end{align}$$中间格林函数部分可以求得
$$\begin{align} &\sum_{\vec{k}}\sum_{\omega'} \frac{1}{\mathrm{i} \omega' - \frac{k^2}{2m}} \frac{1}{\mathrm{i}\omega -\mathrm{i} \omega' - \frac{k^2}{2m}} \\ =&\sum_{\vec{k}}\sum_{\omega'} \left[\frac{1}{\mathrm{i} \omega' - \frac{k^2}{2m}} +\frac{1}{\mathrm{i}\omega -\mathrm{i} \omega') - \frac{k^2}{2m}}\right] \frac{1}{\mathrm{i}\omega - \frac{k^2}{m}}\\ =& \sum_{\vec{k}} \frac{-\beta n(\frac{k^2}{2m}) -\beta\left[ n(\frac{k^2}{2m}) + 1\right]} {\mathrm{i}\omega - \frac{k^2}{m}} \end{align}$$当 $T\to 0$ 时, $n(\frac{k^2}{2m}) \to 0$ , 所以就有
$$\begin{align} v_{\mathrm{eff}} = v + v \sum_{\vec{k}} \frac{ 1}{\mathrm{i}\omega - \frac{k^2}{m}} v_{\mathrm{eff}} \end{align}$$Renormalization
Diverge
下面计算 T-matrix 的具体结果. 计算求和, 可求和化积分
$$\begin{align*} &\sum_{\vec{k}}\frac{1}{E -\frac{\hbar^2k^2}{m}+\mathrm{i}0^+}\\ \approx & \frac{v}{(2\pi)^3}\cdot \int_0^{ + \infty } \mathrm{d}k\cdot 4\pi k^2 \frac{1}{E -\frac{\hbar^2k^2}{m}+\mathrm{i}0^+} \end{align*}$$被积函数当 $k\to \infty$ 时 $\to \infty$ , 积分线性地发散发散, 此时 $T(E) \to 0$ . 而 T-matrix 与散射振幅, 微分截面之间的关系为( Supplementary 中有推导 )
$$\begin{align} \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = \left( \frac{\mu v}{2\pi\hbar^2} \right)^2 |T|^2 = |f(\vec{k}',\vec{k}) |^2 \end{align}$$两体散射中得到 s 波散射振幅为
$$\begin{align} f_s(\theta) = -\frac{1}{1/a_s +\mathrm{i}k} \end{align}$$所以散射截面和散射振幅也 $\to 0$ , 也就是没有散射.
Renormalization
没有散射了, 那算了半天不白算了. 不过, 这也是意料之路的发散, 因为之前在 Pseudopotential 一节中就已经得出过结论, 一个简单的 $g\delta^3(\vec{r})$ 形 式的势是没法给出低能散射的性质的.
所以, 要对上面的结果进行处理, 方法就是 Renormalization .具体如下.
可以加上一项抵消掉发散, 把发散单独拿出来, 然后对比令发散为一个已知的物 理常数. 即
$$\begin{align*} T(E) = \frac{1}{\frac{v}{g}+ \sum_{\vec{k}} \frac{1}{\hbar^2k^2/m}- \sum_{\vec{k}}\left( \frac{1}{E - \frac{\hbar^2k^2}{m}+\mathrm{i}0^+} +\frac{1}{\hbar^2k^2/m} \right)} \end{align*}$$此时, 求和就不再发散, 可以如下求出
$$\begin{align*} & \sum_{\vec{k}}\left( \frac{1}{E - \frac{\hbar^2k^2}{m}+\mathrm{i}0^+} +\frac{1}{\hbar^2k^2/m} \right) \\ \approx& \frac{v}{(2\pi)^3}\int_0^{ + \infty} \mathrm{d}k \cdot 4\pi k^2\cdot\left( \frac{1}{E - \frac{\hbar^2k^2}{m}+\mathrm{i}0^+} +\frac{1}{\hbar^2k^2/m} \right) \\ = & \frac{v}{(2\pi)^3}\int_0^{ + \infty} \mathrm{d}k \cdot 4\pi \cdot\left(\mathcal{P} \frac{k^2}{E - \frac{\hbar^2k^2}{m}} +\frac{k^2}{\hbar^2k^2/m} \right) -\mathrm{i}\pi k^2 \delta\left( E- \frac{\hbar^2 k^2}{m} \right) \end{align*}$$先算主值部分( $E > 0$ )
$$\begin{align*} &\int_0^{ + \infty} \mathrm{d}k \cdot \left(\mathcal{P} \frac{k^2}{E - \frac{\hbar^2k^2}{m}} +\frac{k^2}{\hbar^2k^2/m} \right) \\ = & \mathcal{P} \int_0^{ + \infty} \mathrm{d}k \cdot \frac{E}{\hbar^2/m} \cdot(-1) \cdot\left( \frac{1}{\hbar k/\sqrt{m} +\sqrt{E}} +\frac{-1}{\hbar k/\sqrt{m} -\sqrt{E}} \right) \cdot \frac{1}{-2\sqrt{E}} \\ \end{align*}$$括号中积分为
$$\begin{align*} &\mathcal{P} \int_0^{ + \infty} \mathrm{d}k \cdot\left( \frac{1}{\hbar k/\sqrt{m} +\sqrt{E}} - \frac{1}{\hbar k/\sqrt{m} -\sqrt{E}} \right) \\ =& \ln \left| \hbar k/\sqrt{m} +\sqrt{E} \right|_{k=0}^{k= + \infty} - \ln \left| \hbar k/\sqrt{m} -\sqrt{E} \right|_{k=0}^{k= + \infty} \\ =&0 \end{align*}$$所以主值部分为 $0$ . 再看虚部的 Dirac Delta 函数. 根据公式
$$\begin{align} \delta[f(x)] = \sum_{x_i} \frac{\delta(x-x_i)}{|f'(x_i)|} \end{align}$$其中 $x_i$ 为 $f(x)$ 的零点, 即 $f(x_i)=0$ . 可得
$$\begin{align*} \delta(E - \frac{\hbar^2 k^2}{m}) = \frac{\delta (k - \sqrt{\frac{mE}{\hbar^2}}) + \delta (k + \sqrt{\frac{mE}{\hbar^2}}) }{2\hbar \sqrt{E/m}} \end{align*}$$所以最终有
$$\begin{align*} &\frac{v}{(2\pi)^3}\int_0^{ + \infty} \mathrm{d}k \cdot 4\pi \cdot\left(\mathcal{P} \frac{k^2}{E - \frac{\hbar^2k^2}{m}} +\frac{k^2}{\hbar^2k^2/m} \right) -\mathrm{i}\pi k^2 \delta\left( E- \frac{\hbar^2 k^2}{m} \right) \\ = & -\mathrm{i}\frac{v}{4\pi \hbar^3}m\sqrt{mE} = -\mathrm{i}\frac{vmk}{4\pi\hbar^2} \end{align*}$$最后一个等号利用了 $k = \sqrt{2\mu E/\hbar^2} =\sqrt{m E/\hbar^2}$ .将以上结果代 入 $T(E)$ 的表达式得
$$\begin{align*} T(E) = \frac{1}{\frac{v}{g}+ \sum_{\vec{k}}\frac{1}{\hbar^2k^2/m}+ \mathrm{i}\frac{vmk}{4\pi\hbar^2}} \end{align*}$$又有
$$\begin{align} \left( \frac{mv}{4\pi\hbar^2} \right)^2 |T|^2 = |f(\vec{k}',\vec{k}) |^2 = \left| -\frac{1}{1/a_s +\mathrm{i}k} \right|^2 \end{align}$$式其中代入了 $\mu =m/2$. 所以若令
$$\begin{align} \frac{m}{4\pi \hbar^2 a_s} = \frac{1}{g} + \frac{1}{v}\sum_{\vec{k}} \frac{1}{\hbar^2k^2/m} \end{align}$$那么通过一个 $g\delta^3(\vec{r})$ 形式的势, 就能够给出低能 s 波散射的微分截 面和散射振幅.
Supplementary
The Derivative of T-matrix
Intro
现根据将散射问题作为含时微扰的方法推导 T-matirx 的表达式
$$\begin{align} T = V + V \frac{1}{E_i-H_0 +\mathrm{i}0^{ +}} T \end{align}$$Transition Amplitude
考虑单个粒子在势场 $V(\vec{r})$ 中的运动, Hamiltonian 为
$$\begin{align} H = H_0 + V(\vec{r}) = \frac{\hat{\vec{p}}^2}{2m} + V(\vec{r}) \end{align}$$在 Dirac 表象中, 从 $t_0$ 到 $t$ 时刻的演化为
$$\begin{align} |\psi(t)_D\rangle = U_D(t,t_0) | \psi(t_0)_D\rangle \end{align}$$演化算符由以下运动方程决定
$$\begin{align} \mathrm{i}\hbar \frac{\partial}{\partial t} U_D(t,t_0) = V_D(t) U_D (t,t_0) \end{align}$$形式上有迭代解
$$\begin{align} U_D(t,t_0) = 1 + \frac{1}{\mathrm{i}\hbar}\int_{t_0}^t V_D(t') U_D(t',t_0) \cdot\mathrm{d}t' \end{align}$$T-matrix 的定义与 Transition Amplitude 有关. Transition Amplitude 就是 Dirac 演化算符在 $H_0$ 的本征态构成的 Hilbert 空间中的矩阵元, 即
$$\begin{align} \langle n |U_D(t,t_0) |i\rangle = \delta_{ni} +\frac{1}{\mathrm{i}\hbar} \sum_m \langle n | V |m \rangle \int_{t_0}^t e^{\mathrm{i}\omega_{nm}t'} \langle m | U_D(t',t_0)|i \rangle \cdot \mathrm{d} t' \end{align}$$其中 $|n\rangle, |i\rangle, |m\rangle$ 都是 $H_0$ 的本征态, 对应本征能量为 $E_n, E_i, E_m$ . 同时用了记号 $\omega_{nm} =(E_n-E_m)/\hbar$ . 在第二项中插入了一组 $H_0$ 的一组完备基.
如果将积分中的 $\langle m| U_D(t',t_0)| i \rangle$ 只近似取到首阶, 也就是取 $\langle m| U_D(t',t_0)| i \rangle = \delta_{mi}$ , 那么 Transition Amplitude 就近似为
$$\begin{align} \langle n |U_D(t,t_0) |i\rangle \approx \delta_{ni} +\frac{1}{\mathrm{i}\hbar} \langle n | V |i \rangle \int_{t_0}^t e^{\mathrm{i}\omega_{ni}t'} \cdot \mathrm{d} t' \end{align}$$Definition of T-matrix
T-matrix 的定义就是, 如果将上式中的 $\langle n|V| i\rangle$ 换为 T-matrix $\langle n |T |i\rangle$ , 等式就变为严格相等, 也就是说 T-matrix 由下式定义
$$\begin{align} \langle n |U_D(t,t_0) |i\rangle = \delta_{ni} +\frac{1}{\mathrm{i}\hbar} \langle n | T |i \rangle \int_{t_0}^t e^{\mathrm{i}(\omega_{ni} -\mathrm{i}0^{ + })t'} \cdot \mathrm{d} t' \end{align}$$加入了收敛因子 $\mathrm{i}0^+$ , 它保证 $t\to \infty$ 时被积函数 $\to 1$ , 而 $t_0\to -\infty$ 时 被积函数 $\to 0$ , 关于 $\mathrm{i}0^+$ 更加详细的讨论可 以参考另一篇博客 "多体物理读书会:格林函数分母中无穷小的来源" . 以下采 用简单记法, 记 $T_{ni} = \langle n | T |i \rangle$
上式中, 当 $t\to \infty, t_0\to -\infty$ 时, Transition Amplitude 就定义为 S-matrix , 即
$$\begin{align} S_{ni} = \langle n| S |i\rangle = \delta_{ni} +\frac{1}{\mathrm{i}\hbar} \langle n | T |i \rangle \delta(\omega_{ni}) = \delta_{ni} - 2\pi \mathrm{i} \delta(E_n-E_i) T_{ni} \end{align}$$这样也得了的 S-matrix 和 T-matrix 的关系. 同时, 由于第二项中的 Dirac Delta 函数的存, 只有 $E_n = E_i$ 的 T-matrix 才有实际物理意义. 对于 $E_n = E_i$ 的 T-matrix 称为是 on-shell 的, 因为如果是在 $\vec{k}$ 空间, 能量相同的 $\vec{k}$ 对应于一个球壳.
T-matrix and Cross Section
Physical Meaning of Transition Amplitude
如果问, 假设一个系统在 $t_0$ 时处于某个本征态 $| a \rangle$ , 问在 $t$ 时刻 对其进行测量, 处于本征态 $| b \rangle$ 的概率是多少? 答案将是
$$\begin{align} |\langle b | U(t,t_0) | a \rangle|^2 \end{align}$$如果把 $U$ 换成是 $U_D$ , 结果是一样的, 即
$$\begin{align} |\langle b | U_D(t,t_0) | a \rangle|^2 = \left| e^{\mathrm{i}(E_bt-E_at_0)/\hbar} \langle b| U(t,t_0)|a\rangle \right|^2 = |\langle b | U(t,t_0) | a \rangle|^2 \end{align}$$所以 Transition Amplitude 的模方就是: 一个系统在 $t_0$ 时处于某个本征 态 $| a \rangle$ , 问在 $t$ 时刻对其进行测量, 处于本征态 $| b \rangle$ 的概率.
Transition Rate
Transition rate 定义为
$$\begin{align} \omega(i\to n) = \frac{\mathrm{d}}{\mathrm{d}t}|\langle n | U_D(t,-\infty) | i \rangle|^2 \end{align}$$也就是单位时间的跃迁概率. 当 $i\neq n$ 时, 将 $\langle n | U_D (t,-\infty)| i \rangle = \frac{1}{\mathrm{i}\hbar} T_{ni} \int_{-\infty}^t e^{\mathrm{i}(\omega_{ni} -\mathrm{i}0^{ + })t'} \cdot \mathrm{d} t'$ 代入上式可得
$$\begin{align*} \omega(i\to n) =& \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{1}{\hbar^2}|T_{ni}|^2 \left|\frac{e^{\mathrm{i}(\omega_{ni}-\mathrm{i}0 ^+ )t}}{\mathrm{i}\omega_{ni} + 0^+} \right|^2 \right]\\ =& \frac{\mathrm{d}}{\mathrm{d}t}\left[\frac{1}{\hbar^2}|T_{ni}|^2 \frac{e^{2\cdot 0^+t}}{\omega_{ni}^2 + 0^{+2}} \right]\\ =& \frac{1}{\hbar^2}|T_{ni}|^2 \frac{2\cdot 0^+e^{2\cdot 0^+t}}{\omega_{ni}^2 + 0^{+2}}\\ = & \frac{2\pi}{\hbar} |T_{ni}|^2 \delta(E_n-E_i) \end{align*}$$Differential Cross Section
Differential Cross Section 微分截面 $\mathrm{d}\sigma(\theta,\phi)/\mathrm{d}\Omega$ 定义为
$$\begin{align} \frac{\mathrm{d}\sigma(\theta,\phi)}{\mathrm{d}\Omega}\mathrm{d}\Omega = \frac{\mathrm{number \,\,of\, \,particles\, \,scattered\, \,into\,\, d}\Omega /\mathrm{sec} }{\mathrm{number \,\, incident / sec/area \,\,in \,\,the\,\, } \vec{\rho}\,\,\mathrm{plane}} \end{align}$$其中 $\vec{\rho}$ plane 表示与入射方向垂直的平面. 也就是单位时间出射到 $\mathrm{d}\Omega$ 内的粒子数, 除以, 单位时间单位面积 入射的粒子数. 单位时间单位面积入射的粒子数就是流密度.
考虑量子力学中的情形, 粒子数由概率表征, 粒子流密度也对应地用概率流密度.
Number of particles scattered into $\mathrm{d}\Omega$ /sec
接下来考虑 $\vec{k}$ 空间的情形. 三维自由粒子的能量简并的, 同一能量本 征值 $E_n$ 可以对应多个 $|\vec{k}\rangle$ .
现在求从 $\vec{k}$ 到 $\vec{k}'$ 的 Transition Rate , 其中 $\vec{k}'$ 的方向限制在了某个立体 角 $\mathrm{d}\Omega$ 内, 即
$$\begin{align*} \sum_{\vec{k}'\in \mathrm{d}\Omega}\omega(\vec{k}\to \vec{k}') =& \frac{2\pi}{\hbar}\sum_{\vec{k}'\in \mathrm{d}\Omega} |T_{E_{\vec{k}},E_{\vec{k}'}}|^2 \delta(E_{\vec{k}'}-E_{\vec{k}}) \\ =&\frac{2\pi}{\hbar} |T(E)|^2 \sum_{\vec{k}'\in \mathrm{d}\Omega} \delta(E_{\vec{k}'}-E_{\vec{k}}) \end{align*}$$其中 $E = \frac{\hbar^2k^2}{2m} = \frac{\hbar^2k'}{2m}$ . 求和如果取遍 所有的 $\vec{k}$ , 那么它就是 Density of States 了.
自由粒子的态密度 $\sum_{\vec{k}'}\delta(E_{\vec{k}'}-E_{\vec{k}})$ 可以如下 计算. 其物理意义为在 $\vec{k}$ 空间中能量为 $E + \mathrm{d} E$ 的态的 个数 $\mathrm{d} N$ 除以 $\mathrm{d} E$ ,即
$$\begin{align*} &\sum_{\vec{k}'}\delta(E_{\vec{k}'}-E_{\vec{k}}) = \frac{\mathrm{d}N}{\mathrm{d}E}\\ =& \frac{4\pi k^2\mathrm{d}k/(\frac{2\pi}{L})^{3}}{\mathrm{d}E} \\ =& \frac{4\pi k^2\mathrm{d}k/(\frac{2\pi}{L})^3}{\frac{\hbar^2}{2m}\cdot 2k\mathrm{d}k} \\ =& \left(\frac{L}{2\pi}\right)^3 \frac{mk}{\hbar^2}\cdot 4\pi \end{align*}$$上式中的 $4\pi$ 来自于对 $\vec{k}$ 空间中的一个等能量球面的角度的积分. 计算 Differential Cross Section 只需要得到 $\vec{d}\Omega$ 角度内的概率, 只需要将 $4\pi$ 换成 $\vec{d}\Omega$ 即可.
所以
$$\begin{align*} &\mathrm{number \,\,of\, \,particles\, \,scattered\, \,into\,\, d}\Omega /\mathrm{sec} \\ =& \sum_{\vec{k}'\in \mathrm{d}\Omega}\omega(\vec{k}\to \vec{k}') \\ =& \frac{2\pi}{\hbar} |T(E)|^2\cdot\left(\frac{L}{2\pi}\right)^3 \frac{mk}{\hbar^2} \cdot \mathrm{d}\Omega \end{align*}$$Number incident /sec/area in the $\vec{\rho}$ plane
接着计算入射的概率流密度
$$\begin{align} \vec{\jmath}(\vec{x},t) = \frac{\hbar}{m} \mathrm{Im} (\psi^{*}\nabla \psi) \end{align}$$而对于自由平面波有
$$\begin{align} \psi = \frac{1}{L^{3/2}} e^{\mathrm{i}\vec{k}\cdot \vec{x} -\mathrm{i}Et/\hbar} \end{align}$$所以有
$$\begin{align} \mathrm{number \,\, incident / sec/area \,\,in \,\,the\,\, } \vec{\rho}\,\,\mathrm{plane}= j(\vec{k},t) = \frac{\hbar k}{m}\frac{1}{L^3} \end{align}$$上式中概率流密度的方向已经选定, 只考虑 $\vec{j}(\vec{k},t)$ 其大小即可.
Result
最终得到了 Differential Cross Section
$$\begin{align*} \frac{\mathrm{d}\sigma(\theta,\phi)}{\mathrm{d}\Omega} =& \frac{\mathrm{number \,\,of\, \,particles\, \,scattered\, \,into\,\, d}\Omega /\mathrm{sec} }{\mathrm{number \,\, incident / sec/area \,\,in \,\,the\,\, } \vec{\rho}\,\,\mathrm{plane}} \cdot\frac{1}{\mathrm{d}\Omega} \\ =& \frac{\frac{2\pi}{\hbar} |T(E)|^2\cdot\left(\frac{L}{2\pi}\right)^3 \frac{mk}{\hbar^2} \cdot \mathrm{d}\Omega}{\frac{\hbar k}{m}\frac{1}{L^3}} \cdot\frac{1}{\mathrm{d}\Omega} \\ =& \left( \frac{mL^3}{2\pi \hbar^2} \right)^2 |T(E)|^2 \end{align*}$$Solving for the T-matrix
Intro
前面已知
$$\begin{align} \langle n |U_D(t,-\infty) |i\rangle = \delta_{ni} +\frac{1}{\mathrm{i}\hbar} \sum_m V_{nm} \int_{-\infty}^t e^{\mathrm{i}\omega_{nm}t'} \langle m | U_D(t',t_0)|i \rangle \cdot \mathrm{d} t' \end{align}$$上式是一个迭代形式的, 如果进行一次迭代, 并且进行迭代时, $\langle m | U_D(t',t_0)|i \rangle$ 一项用前面的 T-matrix 的形式, 而不是上式本身, 即将下 式代入上式
$$\begin{align*} \langle m |U_D(t',-\infty) |i\rangle = & \delta_{mi} + \frac{1}{\mathrm{i}\hbar} T_{mi} \int_{-\infty}^{t'} e^{\mathrm{i}(\omega_{mi} - \mathrm{i}0 ^+)t''} \cdot \mathrm{d} t'' \\ =& \delta_{mi} + \frac{1}{\hbar} T_{mi} \frac{e^{\mathrm{i}\omega_{mi}t'}}{-\omega_{mi}+ \mathrm{i} 0^+} \end{align*}$$得到
$$\begin{align*} \langle n |U_D(t,-\infty) |i\rangle =& \delta_{ni} + \frac{1}{\mathrm{i}\hbar} V_{ni} \int_{-\infty}^{t } e^{\mathrm{i}(\omega_{ni} - \mathrm{i}0 ^+)t'} \cdot \mathrm{d} t' \\ &+\frac{1}{\hbar}\frac{1}{\mathrm{i}\hbar} \sum_m V_{nm} \frac{T_{mi}}{-\omega_{mi} + \mathrm{i}0^+} \int_{-\infty}^{t } e^{\mathrm{i}(\omega_{ni}-\mathrm{i} 0 ^+)t'} \cdot \mathrm{d} t' \\ =&\delta_{ni} + \left( V_{ni} + \frac{1}{\hbar} \sum_m V_{nm} \frac{T_{mi}}{-\omega_{mi} + \mathrm{i}0^+} \right) \frac{1}{\mathrm{i}\hbar}\int_{-\infty}^{t } e^{\mathrm{i}(\omega_{ni} - \mathrm{i}0 ^+)t'} \cdot \mathrm{d} t' \\ \end{align*}$$对比前面两式可得
$$\begin{align*} T_{ni} = &V_{ni} + \frac{1}{\hbar} \sum_m V_{nm} \frac{T_{mi}}{-\omega_{mi} + \mathrm{i}0^+} \\ =& V_{ni} + \sum_m V_{nm} \frac{T_{mi}}{E_i-E_m + \mathrm{i}0^+} \end{align*}$$Lippmann-Schwinger Equation
上面的式子可以看成是一个方程组, $T_{ni}$ 可以由已知的矩阵元 $V_{nm}$ 的线性组合得出. 即
$$\begin{align} T_{ni} = \sum_m V_{nm} C_m \end{align}$$接下来用系数 $C_m$ 构造一个态 $|\psi^+\rangle$ . 选取 $H_0$ 的本征态为基底, 即
$$\begin{align} |\psi^+\rangle = \sum_m C_m |m\rangle \end{align}$$那么
$$\begin{align} C_m = \langle m | \psi^+\rangle \end{align}$$将上式代入 $T_{ni}$ 的解得
$$\begin{align} T_{ni} = \sum_m \langle n | V | m \rangle \langle m | \psi^+ \rangle = \langle n | V |\psi^+ \rangle \end{align}$$可以看出, $|\psi^+ \rangle$ 和 $i$ 有关, 即与入射态有关. 将上式代入前面得到的 T-matrix 的迭代方程, 可得
$$\begin{align} \langle n | V |\psi^+ \rangle = \langle n |V|i\rangle + \sum_m \langle n |V|m\rangle \frac{\langle m | V |\psi^+ \rangle} {E_i-E_m + \mathrm{i}0^+} \end{align}$$上式对于所有的 $\langle n |$ 都成立, 所以 $\langle n |V$ 可以去掉, 得到
$$\begin{align} |\psi^+ \rangle = |i\rangle + \sum_m |m\rangle \frac{\langle m | V |\psi^+ \rangle} {E_i-E_m + \mathrm{i}0^+} \end{align}$$$E_m$ 是 $H_0$ 对应本征态 $|m\rangle$ 的本征值, 所以
$$\begin{align} |\psi^+ \rangle =& |i\rangle + \sum_m \frac{1} {E_i-H_0 + \mathrm{i}0^+}|m\rangle\langle m | V |\psi^+ \rangle \\ =& |i\rangle + \frac{1} {E_i-H_0 + \mathrm{i}0^+} V |\psi^+ \rangle \end{align}$$上式即为 Lippmann-Schwinger Equation .
Another Definition of T-matrix
由于
$$\begin{align} \langle n |T | i \rangle= T_{ni} = \langle n | V |\psi^+ \rangle \end{align}$$而 $| \psi^+ \rangle$ 可以用 Lippmann-Schwinger Equation 定义, 所以 T-matrxi 也 可以用 $| \psi^+ \rangle$ 来定义, 即
$$\begin{align} T|i\rangle = V |\psi^+\rangle \end{align}$$将 $V$ 从左边作用在 Lippmann-Schwinger Eqaution 可得
$$\begin{align} T = V + V \frac{1}{E_i-H_0 +\mathrm{i} 0^{ + }} T \end{align}$$上式已经将右边的 $|i\rangle$ 省略. 这样就得到了 T-matrix 的一个简单明了的迭 代方程.
The Scattering Amplitude
将 Lippmann-Schwinger Equation 投影到坐标表象. 考虑到 $H_0$ 在能量的 本征表象对角, $V$ 是 local 的, 所以插入两组能量表象的完备基和一组坐标 表象完备基, 就变成
$$\begin{align} \langle \vec{r}_1|\psi^+ \rangle = \langle \vec{r}_1 |i\rangle + \int \mathrm{d}^3 \vec{r}_2 \sum_{\vec{q}_1 \vec{q}_2}\langle \vec{r}_1 |\vec{q}_1 \rangle \langle \vec{q}_1 | \frac{1} {E_i-H_0 + \mathrm{i}0^+} |\vec{q}_2\rangle \langle \vec{q}_2 | \vec{r}_2\rangle \langle \vec{r}_2 | V |\psi^+ \rangle \end{align}$$能量的本征波函数 $\langle \vec{r} |\vec{k}\rangle = \psi_{\vec{k}}(\vec{r}) = e^{\mathrm{i}\vec{k}\cdot \vec{r}}$ 代入上式 得
$$\begin{align} \langle \vec{r}_1|\psi^+ \rangle = \langle \vec{r}_1 |i\rangle + \frac{2m}{\hbar^2} \int \mathrm{d}^3 \vec{r}_2 \sum_{\vec{q}} \frac{e^{\mathrm{i}\vec{q}\cdot(\vec{r}_1-\vec{r}_2)}}{k^2-q_2 + \mathrm{i} 0^+} \cdot \langle \vec{r}_2 | V |\psi^+ \rangle \end{align}$$求和的部分即为 Green's Function , 可以由留数定理得出
$$\begin{align} G_+(\vec{r}_1, \vec{r}_2) = \sum_{\vec{q}} \frac{e^{\mathrm{i}\vec{q}\cdot(\vec{r}_1-\vec{r}_2)}}{k^2-q_2 + \mathrm{i} 0^+} = -\frac{1}{4\pi} \frac{e^{\mathrm{i}q r_{12}}}{r_{12}} \end{align}$$其中 $r_{12} = |\vec{r}_1- \vec{r}_2|$ . 代回前一式
$$\begin{align} \langle \vec{r}_1|\psi^+ \rangle = \langle \vec{r}_1 |i\rangle - \frac{1}{4\pi} \frac{2m}{\hbar^2} \int \mathrm{d}^3 \vec{r}_2 \frac{e^{\mathrm{i}q r_{12}}}{r_{12}} \cdot V(\vec{r}_2) \langle \vec{r}_2 |\psi^+ \rangle \end{align}$$在离散射中心很远的地方, 即 $|\vec{r}_1| \gg |\vec{r}_2|$ 时, 可做小量 近似
$$\begin{align} r_{12} = \sqrt{ r_1^2 +r_2^2 -2 \vec{r}_1\cdot \vec{r}_2 } \approx r_1 - \frac{\vec{r}_1 \cdot \vec{r}_2}{r_1} \end{align}$$所以
$$\begin{align} e^{\mathrm{i}q r_{12}} \sim e^{\mathrm{i}q r_1} \cdot e^{-\mathrm{i}\vec{q}\cdot \vec{r}_2} \end{align}$$其中 $\vec{q}$ 的方向与 $\vec{r}_2$ 方向相同.
所以
$$\begin{align} \langle \vec{r}_1|\psi^+ \rangle \sim & \langle \vec{r}_1 |i\rangle - \frac{1}{4\pi} \frac{2m}{\hbar^2} \int \mathrm{d}^3 \vec{r}_2 \frac{e^{\mathrm{i}q r_{1}}}{r_{12}}\cdot e^{-\mathrm{i}\vec{q}\cdot \vec{r}_2} \cdot V(\vec{r}_2) \langle \vec{r}_2 |\psi^+ \rangle \\ =& \frac{1}{L^{3/2}} \left[ e^{\mathrm{i} \vec{k} \vec{r}_1} + \frac{e^{\mathrm{i}q r_{1}}}{r_{12}} \cdot f(\vec{q},\vec{k}) \right] \end{align}$$其中
$$\begin{align} f(\vec{q}, \vec{k}) = -\frac{1}{4\pi}\frac{2m}{\hbar^2} L^3 \langle \vec{q} | V | \psi ^+ \rangle \end{align}$$而
$$\begin{align*} \frac{\mathrm{d}\sigma(\theta,\phi)}{\mathrm{d}\Omega} =& \left( \frac{mL^3}{2\pi \hbar^2} \right)^2 |T(E)|^2\\ =& \left( \frac{mL^3}{2\pi \hbar^2} \right)^2 |\langle n | V| \psi^+ \rangle|^2 \end{align*}$$对比以上两式可得
$$\begin{align} \frac{\mathrm{d}\sigma}{\mathrm{d}\Omega} = |f(\vec{q},\vec{k})|^2 \end{align}$$Reference
所有内容基于 Ran Qi 老师上课的笔记
J. J Sakurai, Jim Napolitano, Modern Quantum Mechanics 2ed:
- Chap 2.2 The Schrodinger Versus Heisenberg Picture - Base Kets and Transition Amplitudes
- Chap 5.7 Time-Dependent Perturbation Theory
- Chap 6.1 Scattering as a Time-Dependent Perturbation
- Chap 6.2 the Scattering Amplitude
R. Shankar, Principles of Quantum Mechanics 2ed:
- Chap 19.2 Recapitulation of One-Dimensional Scattering and Overview
- Chap 19.4 Born Again (The Time-Independent Description)
前置技能
- 主值积分
- Dirac 表象
